INTRODUCTION

Researchers conduct Genetic-Wide Association Studies (GWAS) to locate genetic variants (usually SNPs: single nucleotide polymorphisms) responsible for common and complex diseases. An insufficient sample will result in a lack of statistical power, which can prevent researchers from identifying SNPs related to such diseases. Therefore, before conducting a GWAS, investigators frequently calculate the ‘required’ sample size to achieve a specified or the statistical power of available samples. Many investigators have no information on how to calculate the required power to conduct GWAS.

In general, power is calculated by specifying a statistical test, e.g., analysis of variance, an effect size to be detected by the test, and the probability of incorrectly rejecting the null (no effect) hypothesis. The researcher wishes to reject the null hypothesis when the alternative hypothesis (effect of specified size) is true. The statistical power of a test is the probability of rejecting the null hypothesis when it is false (accept the alternative hypothesis). In genetic association studies, the power calculation depends on genotype frequencies and the average effect of each genotype. Because GWAS evaluate hundreds of thousands of associations, it is unrealistic to specify gene frequencies and gene effects for each test and some simplification is needed. Herein, we describe how to calculate power to test for an association between a quantitative trait and genotypes by an analysis of variance (ANOVA). To describe the effect size of SNP’s genotypes on quantitative traits, non-centrality parameter (NCP) is used. The NCP defines the effect size in an ANOVA (Lehmann, 1986). Once a NCP is computed, the power calculation is a function call that computes the cumulative probability of a non-central F distribution, a widely available function. Thus, 1) it is easy to compute power for an F-test of phenotype differences among genotypes. 2) It is easy to implement this calculation in many statistical software packages. If the function is unavailable, there are good numerical approximations that are not difficult to program (Abramowitz and Stegun, 1965; Johnson et al., 1995).

In this paper, we explain how to compute a NCP based on genetic concepts of phenotype heritability, additive allele effects, or dominant/recessive allele effects. We illustrate the basic power calculations coded in Mathematica, Matlab, R, SAS and Stata. We outline algorithms to plot power as a function of heritability and implement the algorithm in SAS. We outline algorithms to plot the effect size detected with power of 0.8 as a function of minor allele frequency and implement the algorithm in Matlab. Our approach relates the statistically relevant NCP to genetically relevant parameters to provide better insight into the power of a study to identify genetic variants associated with quantitative traits.

Although there are several stand-alone packages that can compute power (Dupont and Plummer, 1990, 1998; Faul et al., 2007; Feng et al., 2011; Gauderman, 2002; Purcell et al., 2003; Spencer et al., 2009), learning how to use them takes time and they tend to lack flexibility. Our goal is to make the power calculation straightforward for someone who is familiar with any of the common statistical packages.

METHODS

We assume that associations between a continuous phenotype, e.g., blood pressure, and many genetic markers will be tested one at a time by analysis of variance (ANOVA). Table 1 is a generic ANOVA summary of the analysis for a single marker. Several terms of interest to the discussion of the statistical power of these analyses are symbolized in this table. The table assumes that phenotypes and genotypes are measured in n subjects. The degrees of freedom for genotypes, d, will depend on how we evaluate the genotypes, but typically d will be 1 or 2.

The p covariates are incorporated to adjust for non-genetic factors that may affect the phenotype. In the case of blood pressure for example, these might be covariates that adjust for age, blood pressure medication, and population stratification. The same covariate adjustment is applied to the analysis of each genetic marker. So operationally the phenotype measurements are initially adjusted by these covariates and the marker-specific computations are usually run on the residuals after the covariate adjustment. An ANOVA test of ‘no gene association’ tests the null hypothesis that there are no phenotype differences among genotypes, i.e., η² = 0. Here, η² symbolizes the effect size, which is a summary of the magnitude of the phenotype differences among genotypes. The power of this F-test can be computed using functions that are widely available in statistical software packages. Power depends on the magnitude of a so-called non-centrality parameter (NCP), λ = η² ⁄ σ², the degrees of freedom, d and ν, and the significance level, α. In particular, the power of this test is computed as the probability that the F-ratio will exceed a value, Power  = Pr[F(d, ν, λ) ≥ c], where F(d, ν, λ) denotes a random variable with a non-central F distribution and c denotes the value of an F-ratio that is statistically significant at the α–level, i.e., c such that α = Pr[F(d, ν, λ = 0) ≥ c]. These two values, Power and c, can be calculated in many software packages, e.g., SAS or Matlab. Thus, it is straightforward to compute power for an F-test of phenotype differences among genotypes when we specify a NCP. Unfortunately a NCP does not provide an insightful interpretation of the effect size in the context of a GWAS that seeks to identify differences in a continuous phenotype associated with single nucleotide polymorphisms (SNP).

NCP as a Function of Heritability

Our initial aim is to relate the non-centrality parameter to the proportion of variation that is explained by the SNP, \(R^{2}\). When the computations are run on the residuals after covariate adjustment, \(R^{2}\)is simply the R-squared associated with adding genotype. With respect to entries in Table 1, this is the observed proportion of the phenotype variation that is explained by the SNP genotypes after adjusting for the covariates,

\[R^{2} = \frac{SS_{\text{genotypes}}}{SS_{\text{genotypes}} + SS_{\text{residual}}}\]

The expected value of a non-central F-distribution is:

\[\mu_{F} = \frac{\nu\left( d + \lambda \right)}{d\left( \nu - 2 \right)}\]

The expected F is a one-to-one function of the non-centrality parameter,\(\lambda\), and consequently specifying\(\mu_{F}\)is equivalent to specifying the non-centrality parameter, specifically

\[\lambda = \frac{d\left( \nu - 2 \right)}{\nu}\mu_{F} - d\]

The ‘true’ proportion of the phenotype variation (after adjustment for covariates) that is explained by the genotypes is denoted \(\pi_{R}\). Replacing the F-ratio in Table 1 with the expectations,

\[\mu_{F} = \frac{\nu}{d}\frac{\pi_{R}}{1 - \pi_{R}}\]

yields a relationship that specifies the non-centrality parameter as a function of the expected proportion of the phenotype variation that is explained by the genotypes, i.e.,

Genetic Models

The entries in Table 1 assume a simple model for phenotype heritability where each genotype yields a phenotype that has a normal distribution with genotype-specific mean and a variance that is the same across genotypes. For our purpose here, it is convenient to assume that there are two alleles, one of which has an allele frequency less than or equal to the other, a.k.a. minor allele. The genotype frequencies of SNPs are usually unknown at the experimental design stage. However for power calculations, we approximate genotype frequencies in terms of their minor allele frequency (MAF), and further assume that genotypes are in Hardy-Weinberg equilibrium. That is, genotype frequencies for the genotype with 0, 1, or 2 minor alleles,\(\left\{ f_{0},f_{1},f_{2} \right\}\), are approximated by \(\left\{ \left( 1 - q \right)^{2},2q\left( 1 - q \right),q^{2} \right\}\) where q is the MAF. Under this model, \(\eta^{2} = n\sum_{a = 0}^{2}{f_{a}\left( \mu_{a} - \overline{\mu} \right)^{2}}\), where \(\mu_{a}\)designates the mean value of the phenotype distribution for a genotype with ‘a’ minor alleles. In this general setting, the task of specifying \(\mu_{a}\) for every marker is too tedious to be useful, and we recommend the preceding approach for obtaining the NCP. However, there are two genetic models which provide straightforward interpretations.

NCP in an Additive Genetic Model

An additive genetic model assumes that alleles have an additive effect on the phenotype and our assumptions allow us to relate the NCP to the trend in the phenotype means, \(\beta\), with the number of minor alleles. To model this, we count the number of a specified allele in the genotype, x_a = 0, 1, 2, and write the phenotype means as μ_a = μ₀ + βx_a. Note that this formulation implies that μ = μ₀ + βx and μ_a − μ = β(x_a − x). The test for a trend in the phenotype with increasing count of minor alleles is a test that \(\beta = 0\). In the context of Table 1, this trend test corresponds to \(d = 1\) and

\[\eta^{2} = n\beta^{2}\sum_{a = 0}^{2}{f_{a}\left( x_{a} - \overline{x} \right)^{2}}\]

where \(f_{a}\) is the genotype frequency and \(\beta\) is the slope of the trend (change in phenotype mean per minor allele). These assumptions allow us to relate the effect size, \(\frac{\beta}{\sigma}\), to the NCP,

NCP in dominant/recessive models

We can co-opt the previous results to apply to dominant genetic models. If the minor allele is dominant, let

\[x_{a} = \left\{ \begin{matrix} 0\ if\ a = 0 \\ 1\ otherwise, \\ \end{matrix} \right.\ \]

and if the minor allele is recessive let

\[x_{a} = \left\{ \begin{matrix} 1\ if\ a = 0 \\ 0\ otherwise. \\ \end{matrix} \right.\ \]

with either off these changes to the definition of \(x_{a}\), the NCP can be computed using the same formulae as the additive genetic model. However the interpretation of the slope parameter,\(\text{\ β}\), changes to the difference between the phenotype means of the dominant genotypes and the recessive genotype, respectively. Note that the power is the same whether the minor allele is dominant or recessive since \(\beta\) computed under the dominant assumption simply becomes \(- \beta\) under the recessive assumption; both yield the same NCP power is the same whether the minor allele is dominant or recessive since \(\beta\) computed under the dominant assumption simply becomes \(- \beta\) under the recessive assumption; both yield the same NCP.

Figure 1. Computer code in SAS, Matlab, R, Stata, and Mathematica that compute power for an ANOVA (Table 1)

RESULTS

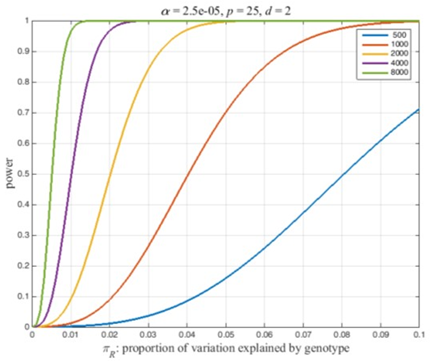
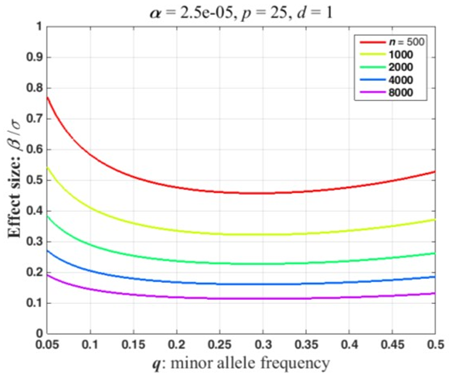
Power is the probability of a significant ANOVA under the alternative hypothesis, i.e., Pr(F c) where F denotes a random variable with a non-central F-distribution, F(d, n-p-d, NCP), and c is the value that is significant at the a-level : Critical Value. Power and c can be calculated in many software packages. Figure 1 illustrates the fundamental power calculation coded in several well-known computer packages. The codes in Figure 2 outlines the basic power calculation. The user specifies the type 1 error (significance level), sample size (n), number of adjusting covariates (p), the numerator degrees of freedom (d), and the NCP. Typically a marker SNP has two alleles and a minor allele frequency (MAF) exceeding 5%. In a large sample, n = 1000, at least a few individuals of the three possible genotypes should be present in the sample giving the degrees of freedom for genotypes, \(d\)= 2. The code in Figure 1 can be embedded in a loop that varies the NCP as a function of the expected proportion of the variation that is explained by the genotypes (Eqn 1) or as a function of \(\frac{\beta}{\sigma}\) (Eqn 2). Figure 2 plots power curves based on the expected proportion of the variation that is explained by the genotypes. This figure iterates the preceding code for sample sizes, n = 500, 1000, 2000, 4000, 8000, and NCP defined by Eqn 1 with \(\pi_{R}\) = 0 to 0.01 by 0.001. Figure 2 was produced using Matlab as the authors are more adept at plotting using this programming language. SAS code that will reproduce the essential features of Figure 2 are included in the appendix. Because the NCP in Eqn 2 also depends on the MAF, we report the effect size, \(\frac{\beta}{\sigma}\), that has a power of 0.8 as a function of the MAF. Conceptually, this could be computed by adding another loop that varies the MAF and saving the effect sizes with a power of 0.8. Figure 3 plots the effect size detectable with a power of 0.8 as a function of the MAF for the sample sizes used in Figure 2. This was computed using a Matlab program. The calculations can be finessed to express power in the context of a disease locus that is observed via linked markers. The appended Matlab program incorporates an adjustment for the correlation between a disease locus and the markers.

Figure 2. Power of an ANOVA for several sample sizes as a function of the proportion of the phenotype variation that is explained by the genotypes

Figure 3. Effect size detectable with a power of 0.8 in the dominant/recessive genetic model as a function of the minor allele frequency for several sample sizes

DISCUSSION

In this paper, we described computer codes that calculate the required statistical power for detecting a significant association between a genetic variant and a quantitative trait in GWAS under additive, dominant and recessive models for the phenotype — Power Calculation for SNPs and quantitative trait Association (PCSQT). These codes, i.e. PCSQT, were implemented in five widely used commercial statistical packages. The other statistical methods do not explicitly include this parameter while calculating study power. Our approach relates the statistically relevant NCP to genetically relevant parameters to provide better insight into the identification of genetic variants associated with quantitative traits. If the NCP is specified it is easy to compute statistical power for an F-test of phenotype differences among genotypes that can easily be implemented in many statistical software packages. The calculations can answer the following question: if a Single Nuclear Polymorphism (SNP) explains % of the variation i.e. Heritability, with sample size n, what is the statistical power of the proposed study?

These codes permit investigators to employ heritability as an effect size, instead of the mean of a quantitative trait, which is often unavailable in genetic studies. To calculate power, we use the following parameters: (2) Total sample size; (2) Heritability (the range is 0~1); (3) type 1 error rate: (4) number of SNPs in the genetic study: (5) number of covariates; 6) linkage Disequilibrium (LD) r² (Pritchard and Przeworski, 2001): investigators input a LD value between a genetic marker and a hypothesized causative variant. When the LD between the genetic and causative markers is r², the sample size (N) is increased to be N/ r². In other words, to achieve approximately the same power with the genetic marker as is achieved with the causative variant, the sample size must be increased by a factor of 1/ r^2. (Pritchard and Przeworski, 2001).

The output information include: (1) statistical power; (2) a family of power curves plots with different heritability and sample size combinations, as shown in Figure 1. The suggested statistical approach has some limitations. First, population stratification is not considered while calculating statistical power using these codes. Nevertheless, it can be added as one of the covariates while estimating the required power calculation. Second, the effect of the interaction between genetic variants, and environmental factors on the power determination cannot be included in the power calculation. In a GWAS that examines a million SNPs, a Bonferroni adjustment for multiple comparisons implies that the critical value, c, is computed for a significance level on the order of 10^-8 (Klein, 2007). The numerical algorithm implemented in the software to approximate c may or may not be adequate for the task. For the five packages. the software packages in Figure 1, we could not find documentation for the algorithm or the error in the numerical approximation. Mathematica allows one to specify the number of significant digits; we set this to 20 and use this as a standard in Table 2. Table 2 presents an example of critical values computed to 6 decimal places for examined software packages and where the values are computed, all agree except for \(\alpha = 10^{- 12}\). SAS was the only software package that failed to compute the critical values for \(\alpha > 10^{- 5}\). Differences among critical values in Table 2 have little practical importance. In practice, the F-distribution will only approximate the actual distribution of the ratio statistic in an analysis of variance (Table 1). The approximation is satisfactory at conventional significance levels such as 0.05 or 0.01, and p-values computed from the F-distribution are generally accepted as ‘good’ by the scientific community. However, very small p-values, such as 10^-8, imply a degree of approximation to the distribution of the test statistic that is unlikely to be achieved.

Key Points

• Statistical power calculation should be performed before conducting genetic association studies.

• Several stand-alone software packages are available to do power calculations. Many researchers are unfamiliar with these packages while they are familiar with standard statistical packages.

• We demonstrated how to code power calculations in several standard statistical packages—Mathematica, Matlab, R, SAS, Stata—that employ an F-test to determine the required statistical power to detect a statistical relationship between genetic variants and a continuous trait in genetic association studies under additive, dominant and recessive models’ assumptions.

ACKNOWLEDGEMENT

This study is supported by National Heart, Lung, and Blood Institute (NHLBI) under award number 1 R15 HL126074-01. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.